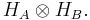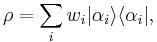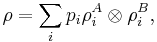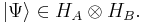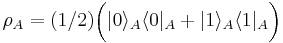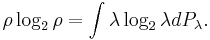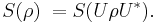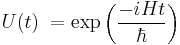Quantum entanglement
| Quantum mechanics | ||||||||||||||||
 |
||||||||||||||||
| Uncertainty principle |
||||||||||||||||
Introduction · Mathematical formulations
|
||||||||||||||||
Quantum entanglement, also called the quantum non-local connection, is a property of the quantum mechanical state of a system containing two or more objects, where the objects that make up the system are linked in a way such that one cannot adequately describe the quantum state of a constituent of the system without full mention of its counterparts, even if the individual objects are spatially separated. This interconnection leads to non-classical correlations between observable physical properties of remote systems, often referred to as nonlocal correlations. During the formation of quantum theory, this property of entanglement was recognized as a direct consequence. Quantum entanglement is at the heart of the EPR paradox that was developed by Albert Einstein, Boris Podolsky, and Nathan Rosen in 1935, and was experimentally verified for the first time in 1980 by the French physicist Alain Aspect.
Contents |
History
Entanglement is one of the properties of quantum mechanics that caused many physicists, including Albert Einstein, to dislike this formulation of quantum mechanical theory. In 1935, responding to Niels Bohr's advocacy that quantum mechanics as a theory was complete, Einstein, Podolsky, and Rosen formulated the EPR paradox. The quantum mechanical thought experiment concluded that either nonlocal interaction exists or quantum mechanics is incomplete as a theory.[1] Einstein famously derided entanglement as "spukhafte Fernwirkung"[2] or "spooky action at a distance".
It was his belief that future mathematicians would discover that quantum entanglement entailed nothing more or less than an error in their calculations. As he once wrote: "I find the idea quite intolerable that an electron exposed to radiation should choose of its own free will, not only its moment to jump off, but also its direction. In that case, I would rather be a cobbler, or even an employee in a gaming house, than a physicist".[3]
In 1964 John Stewart Bell derived an upper limit, known as Bell's inequality, on the strength of correlations for any theory obeying "local realism". According to the inequality, quantum mechanical predictions can lead to correlations stronger than this limit, leading to results that are experimentally distinguishable from the results of a broad class of local hidden-variable theories.
In 1982, Alain Aspect published a paper detailing his experiments showing that nonlocal interactions do occur [4]. This paper and the subsequent experiments since have shown results for which local hidden-variable theories cannot account. However, there may be flaws in experimental design giving rise to problems, known as "loopholes", that bring into question the validity of these experimental findings. High-efficiency and high-visibility experiments are now in progress that should confirm or invalidate the existence of quantum entanglement without the possibility of these "loopholes". For more information, see the article on experimental tests of Bell's inequality.
Concept
When particles decay into other particles, these decays must obey the various conservation laws. As a result, pairs of particles can be generated that are required to be in certain quantum states. For ease of understanding, consider the situation where a pair of these particles are created, have a two state spin and one must be spin up and the other must be spin down. As described in the introduction, these two particles can now be called entangled since you can not fully describe one particle without mentioning the other. This type of entangled pair where the particles always have opposite spin is known as the spin anti-correlated case. The case where the spins are always the same is known as spin correlated.
Now that entangled particles have been created, quantum mechanics also holds that an observable, for example spin, is indeterminate until a measurement is made of that observable. At that instant, all of the possible values that the observable might have had "collapse" to the value that is measured. Consider, for now, just one of these created particles. In the singlet state of two spin, it is equally likely that this particle will be observed to be spin-up or spin-down. Meaning if you were to measure the spin of many like particles, the measurement will result in an unpredictable series of measurements that will tend to a 50% probability of the spin being up or down. However, the results are quite different if you examine both of the entangled particles in this experiment. When each of the particles in the entangled pair is measured in the same way, the results of their spin measurement will be correlated. Measuring one member of the pair tells you what the spin of the other member is without actually measuring its spin.
The controversy surrounding this topic comes in once you consider the ramifications of this result. Normally under the Copenhagen interpretation, the state a particle occupies is determined the moment the state is measured. However, in an entangled pair when the first particle is measured, the state of the other is known at the same time without measurement, regardless of the separation of the two particles. This knowledge of the second particle's state is at the heart of the debate. If the distance between particles is large enough, information or influence might be traveling faster than the speed of light which violates the principle of special relativity. One experiment that is in agreement with the effect of entanglement "traveling faster than light" was performed in 2008. the experiment found the "speed" of quantum entanglement has a minimum lower bound of 10,000 times the speed of light. [5]However, because the method involves uncontrollable observation rather than controllable changing of state, no actual information is transmitted in this process. Therefore, the speed of light remains the communication speed limit.
Other Interpretations
Theories involving hidden variables have been proposed in order to explain this result. These hidden variables would account for the spin of each particle, and would be determined when the entangled pair is created. It may appear then that the hidden variables must be in communication no matter how far apart the particles are, that the hidden variable describing one particle must be able to change instantly when the other is measured. If the hidden variables stop interacting when they are far apart, the statistics of multiple measurements must obey an inequality (called Bell's inequality), which is, however, violated both by quantum mechanical theory and experimental evidence.
If each particle departs the scene of its "entangled creation", however, with properties that would unambiguously determine the value of the quality to be subsequently measured, then the postulated instantaneous transmission of information across space and time would not be required to account for the result of both particles having the same value for that quality. The Bohm interpretation postulates that a guide wave exists connecting what are perceived as individual particles such that the supposed hidden variables are actually the particles themselves existing as functions of that wave.
Yet another interpretation of this phenomenon is that quantum entanglement does not necessarily enable the transmission of classical information faster than the speed of light because a classical information channel is required to complete the process.
Applications of entanglement
Entanglement has many applications in quantum information theory. With the aid of entanglement, otherwise impossible tasks may be achieved. Among the best known applications of entanglement are superdense coding, quantum teleportation, information exchanges through time, and the creation of a quantum computer. Efforts to quantify this resource are often termed entanglement theory.[6][7] Quantum entanglement also has many different applications in the emerging technologies of quantum computing and quantum cryptography, and has been used to realize quantum teleportation experimentally.[8] At the same time, it prompts some of the more philosophically oriented discussions concerning quantum theory. The correlations predicted by quantum mechanics, and observed in experiment, reject the principle of local realism, which is that information about the state of a system can only be mediated by interactions in its immediate surroundings and that the state of a system exists and is well-defined before any measurement. Different views of what is actually occurring in the process of quantum entanglement can be related to different interpretations of quantum mechanics. In the previously standard one, the Copenhagen interpretation, quantum mechanics is neither "real" (since measurements do not state, but instead prepare properties of the system) nor "local" (since the state vector 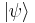 comprises the simultaneous probability amplitudes for all positions, e.g.
comprises the simultaneous probability amplitudes for all positions, e.g. 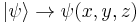 );
);
The Reeh-Schlieder theorem of quantum field theory is sometimes seen as the QFT analogue of quantum entanglement.
Quantum Mechanical Framework
The following subsections are for those with a good working knowledge of quantum mechanics, including familiarity with the theoretical framework developed in the articles: bra-ket notation and mathematical formulation of quantum mechanics.
Pure states
Consider two noninteracting systems  and
and  , with respective Hilbert spaces
, with respective Hilbert spaces 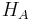 and
and 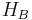 . The Hilbert space of the composite system is the tensor product
. The Hilbert space of the composite system is the tensor product
If the first system is in state 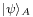 and the second in state
and the second in state 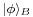 , the state of the composite system is
, the state of the composite system is
States of the composite system which can be represented in this form are called separable states, or (in the simplest case) product states.
Not all states are separable states (and thus product states). Fix a basis 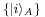 for
for 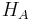 and a basis
and a basis 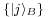 for
for 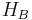 . The most general state in
. The most general state in  is of the form
is of the form
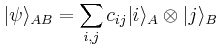 .
.
This state is separable if 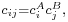 yielding
yielding 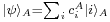 and
and 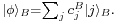 It is inseparable if
It is inseparable if 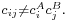 If a state is inseparable, it is called an entangled state.
If a state is inseparable, it is called an entangled state.
For example, given two basis vectors 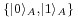 of
of 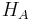 and two basis vectors
and two basis vectors  of
of 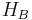 , the following is an entangled state:
, the following is an entangled state:
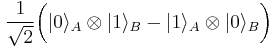 .
.
If the composite system is in this state, it is impossible to attribute to either system  or system
or system  a definite pure state. Instead, their states are superposed with one another. In this sense, the systems are "entangled". This has specific empirical ramifications for interferometry [9]. It is worthwhile to note that the above example is one of four Bell states, which are (maximally) entangled pure states (pure states of the
a definite pure state. Instead, their states are superposed with one another. In this sense, the systems are "entangled". This has specific empirical ramifications for interferometry [9]. It is worthwhile to note that the above example is one of four Bell states, which are (maximally) entangled pure states (pure states of the 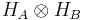 space, but which cannot be separated into pure states of each
space, but which cannot be separated into pure states of each 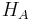 and
and 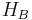 ).
).
Now suppose Alice is an observer for system  , and Bob is an observer for system
, and Bob is an observer for system  . If Alice makes a measurement in the
. If Alice makes a measurement in the 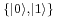 eigenbasis of A, there are two possible outcomes, occurring with equal probability:
eigenbasis of A, there are two possible outcomes, occurring with equal probability:
- Alice measures 0, and the state of the system collapses to
 .
. - Alice measures 1, and the state of the system collapses to
 .
.
If the former occurs, then any subsequent measurement performed by Bob, in the same basis, will always return 1. If the latter occurs, (Alice measures 1) then Bob's measurement will return 0 with certainty. Thus, system B has been altered by Alice performing a local measurement on system A. This remains true even if the systems A and B are spatially separated. This is the foundation of the EPR paradox.
The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see no-communication theorem.
In some formal mathematical settings, it is noted that the correct setting for pure states in quantum mechanics is projective Hilbert space endowed with the Fubini-Study metric. The product of two pure states is then given by the Segre embedding.
Ensembles
As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has a large number of copies of the same system, then the state of this ensemble is described by a density matrix, which is a positive matrix, or a trace class when the state space is infinite dimensional, and has trace 1. Again, by the spectral theorem, such a matrix takes the general form:
where the 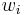 's sum up to 1, and in the infinite dimensional case, we would take the closure of such states in the trace norm. We can interpret
's sum up to 1, and in the infinite dimensional case, we would take the closure of such states in the trace norm. We can interpret 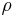 as representing an ensemble where
as representing an ensemble where 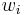 is the proportion of the ensemble whose states are
is the proportion of the ensemble whose states are 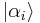 . When a mixed state has rank 1, it therefore describes a pure ensemble. When there is less than total information about the state of a quantum system we need density matrices to represent the state.
. When a mixed state has rank 1, it therefore describes a pure ensemble. When there is less than total information about the state of a quantum system we need density matrices to represent the state.
Following the definition in previous section, for a bipartite composite system, mixed states are just density matrices on 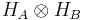 . Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as
. Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as
where 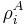 's and
's and 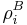 's are themselves states on the subsystems A and B respectively. In other words, a state is separable if it is probability distribution over uncorrelated states, or product states. We can assume without loss of generality that
's are themselves states on the subsystems A and B respectively. In other words, a state is separable if it is probability distribution over uncorrelated states, or product states. We can assume without loss of generality that 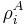 and
and 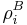 are pure ensembles. A state is then said to be entangled if it is not separable. In general, finding out whether or not a mixed state is entangled is considered difficult. Formally, it has been shown to be NP-hard. For the
are pure ensembles. A state is then said to be entangled if it is not separable. In general, finding out whether or not a mixed state is entangled is considered difficult. Formally, it has been shown to be NP-hard. For the 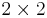 and
and 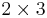 cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.
cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.
Experimentally, a mixed ensemble might be realized as follows. Consider a "black-box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. For example, it could produce two populations of electrons: one with state 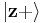 with spins aligned in the positive
with spins aligned in the positive 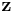 direction, and the other with state
direction, and the other with state 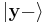 with spins aligned in the negative
with spins aligned in the negative 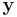 direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.
direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.
Reduced density matrices
The idea of a reduced density matrix was introduced by Paul Dirac in 1930.[10] Consider as above systems  and
and  each with a Hilbert space
each with a Hilbert space 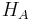 ,
, 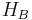 . Let the state of the composite system be
. Let the state of the composite system be
As indicated above, in general there is no way to associate a pure state to the component system  . However, it still is possible to associate a density matrix. Let
. However, it still is possible to associate a density matrix. Let
 .
.
which is the projection operator onto this state. The state of  is the partial trace of
is the partial trace of 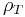 over the basis of system
over the basis of system  :
:
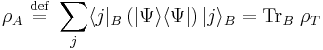 .
.
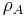 is sometimes called the reduced density matrix of
is sometimes called the reduced density matrix of 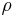 on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.
on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.
For example, the reduced density matrix of  for the entangled state
for the entangled state 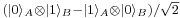 discussed above is
discussed above is
This demonstrates that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of  for the pure product state
for the pure product state 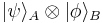 discussed above is
discussed above is
In general, a bipartite pure state ρ is entangled if and only if one, meaning both, of its reduced states are mixed states. Reduced density matrices were explicitly calculated in different spin chains with unique ground state. An example is one dimensional AKLT spin chain: the ground state can be divided into a block and environment. The reduced density matrix of the block is proportional to a projector to a degenerated ground state of another Hamiltonian. The reduced density matrix also was evaluated for XY spin chains.
Entropy
In this section, the entropy of a mixed state is discussed as well as how it can be viewed as a measure of quantum entanglement.
Definition
In classical information theory, the Shannon entropy,  is associated to a probability distribution,
is associated to a probability distribution, , in the following way:
, in the following way:
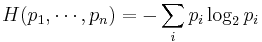 .
.
Since a mixed state ρ is a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:
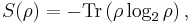 .
.
In general, use the Borel functional calculus to calculate 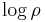 . If ρ acts on a finite dimensional Hilbert space and has eigenvalues
. If ρ acts on a finite dimensional Hilbert space and has eigenvalues 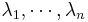 , the Shannon entropy is recovered:
, the Shannon entropy is recovered:
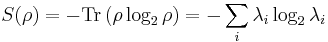 .
.
Since an event of probability 0 should not contribute to the entropy, and given that 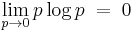 , the convention is adopted that
, the convention is adopted that 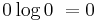 . This extends to the infinite dimensional case as well: if ρ has spectral resolution
. This extends to the infinite dimensional case as well: if ρ has spectral resolution 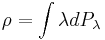 , assume the same convention when calculating
, assume the same convention when calculating
As in statistical mechanics, the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is 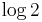 (which can be shown to be the maximum entropy for
(which can be shown to be the maximum entropy for 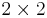 mixed states).
mixed states).
As a measure of entanglement
Entropy provides one tool which can be used to quantify entanglement, although other entanglement measures exist.[7] If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems.
For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure.
It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution {1/n,...,1/n}. Therefore, a bipartite pure state
is said to be a maximally entangled state if there exists some local bases on H such that the reduced state of ρ is the diagonal matrix
For mixed states, the reduced von Neumann entropy is not the unique entanglement measure.
As an aside, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics (comparing the two definitions, we note that, in the present context, it is customary to set the Boltzmann constant 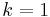 ). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,
). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,
Indeed, without the above property, the von Neumann entropy would not be well-defined. In particular, U could be the time evolution operator of the system, i.e.
where H is the Hamiltonian of the system. This associates the reversibility of a process with its resulting entropy change, i.e. a process is reversible if, and only if, it leaves the entropy of the system invariant. This provides a connection between quantum information theory and thermodynamics. Rényi entropy also can be used as a measure of entanglement.
See also
- Bell test experiments
- Entanglement witness
- Separable states
- Squashed entanglement
- Quantum coherence
- Action at a distance (physics)
- Ghirardi-Rimini-Weber theory
- Quantum pseudo-telepathy
- Entanglement distillation
- Quantum mysticism
- Concurrence (quantum computing)
- Multipartite entanglement
- Photon entanglement
References
Specific references:
- ↑ Einstein A, Podolsky B, Rosen N (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Phys. Rev. 47 (10): 777–780. doi:10.1103/PhysRev.47.777.
- ↑ A. Einstein, The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955, Walker, New York, 1971. (cited in Quantum Entanglement and Communication Complexity (1998), by M. P. Hobson et. al., p.1/13)
- ↑ Fred R. Shapiro, Joseph Epstein (2006). The Yale Book of Quotations. Yale University Press. p. 228. ISBN 0300107986.
- ↑ A. Aspect, P. Grangier, and G. Roger (1982). "Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities". Physical Review Letters 49 (2): 91–94. doi:10.1103/PhysRevLett.49.91.
- ↑ Testing Spooky Action at a Distance Preprint: Testing Spooky Action at a Distance Nature Article
- ↑ Entanglement Theory Tutorials from Imperial College London
- ↑ 7.0 7.1 M.B. Plenio and S. Virmani, An introduction to entanglement measures, Quant. Inf. Comp. 7, 1 (2007) [1]
- ↑ Dik Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred Eibl, Harald Weinfurter & Anton Zeilinger, Experimental Quantum Teleportation, Nature vol.390, 11 Dec 1997, pp.575. (Summarized at http://www.quantum.univie.ac.at/research/photonentangle/teleport/)
- ↑ Jaeger G, Shimony A, Vaidman L (1995). "Two Interferometric Complementarities". Phys. Rev. 51: 54. doi:10.1103/PhysRevA.51.54.
- ↑ Dirac, P. A. M.: Note on Exchange Phenomena in the Thomas Atom. Proc. Cambr. Phil. Soc. 26, 376-385 (1930).
General references:
- Horodecki M, Horodecki P, Horodecki R (1996). "Separability of mixed states: necessary and sufficient conditions". Physics Letters A: 210.
- Gurvits L (2003). "Classical deterministic complexity of Edmonds' Problem and quantum entanglement". Proceedings of the thirty-fifth annual ACM symposium on Theory of computing: 10. doi:10.1145/780542.780545.
- Bengtsson I, Zyczkowski K (2006). "Geometry of Quantum States". An Introduction to Quantum Entanglement. Cambridge: Cambridge University Press.
- Steward EG (2008-03-24). Quantum Mechanics: Its Early Development and the Road to Entanglement. Imperial College Press. ISBN 978-1860949784.
- Horodecki R, Horodecki P, Horodecki M, Horodecki K (2007). "Quantum entanglement". Rev. Mod. Phys.. http://arxiv.org/abs/quant-ph/0702225.
- Jaeger G. (2009). Entanglement, Information, and the Interpretation of Quantum Mechanics Heildelberg: Springer. ISBN 978-3-540-92127-1.
- Plenio MB, Virmani S (2007). "An introduction to entanglement measures". Quant. Inf. Comp. 7, 1 (2007). http://arxiv.org/abs/quant-ph/0504163.
External links
- Quantum Entanglement at Stanford Encyclopedia of Philosophy
- Entanglement experiment with photon pairs - interactive
- Multiple entanglement and quantum repeating
- How to entangle photons experimentally
- Quantum Entanglement and Bell's Theorem at MathPages
- Audio - Cain/Gay (2009) Astronomy Cast Entanglement
- Recorded research seminars at Imperial College relating to quantum entanglement
- How Quantum Entanglement Works
- Quantum Entanglement and Decoherence: 3rd International Conference on Quantum Information (ICQI)
- The original EPR paper
- Ion trapping quantum information processing
- IEEE Spectrum On-line: The trap technique
- Was Einstein Wrong?: A Quantum Threat to Special Relativity
- A creative interpretation of Quantum Entanglement